ごりちゃんがゆく

競プロをするゴリラの精進記録

1からNまでのnについて、nの約数の個数の総和を求める

アルゴリズム

ごり〜

こんばんは
高校数学ぐらいの内容ですが、整理していたらいくつか気づきがあったので記します
唐突ですが、「1からNまでのnについて、nの約数の個数の総和」をどう求めるか？を考えていきたいと思います
N の大きさとしては N \le 10^{12} ぐらいのを高速に求めたいです

なお、この記事で約数の個数とは、正の約数の個数を指します
出てくるグラフも x \gt 0 を定義域としています
ご了承ください

復習

約数

整数N の約数とは、Nを割り切ることのできる整数です
以下、例として1から10までのn について、nの約数を集合で表します

  • 1 の約数： \lbrace 1 \rbrace
  • 2 の約数： \lbrace 1,2 \rbrace
  • 3 の約数： \lbrace 1,3 \rbrace
  • 4 の約数： \lbrace 1,2,4 \rbrace
  • 5 の約数： \lbrace 1,5 \rbrace
  • 6 の約数： \lbrace 1,2,3,6 \rbrace
  • 7 の約数： \lbrace 1,7 \rbrace
  • 8 の約数： \lbrace 1,2,4,8 \rbrace
  • 9 の約数： \lbrace 1,3,9 \rbrace
  • 10 の約数： \lbrace 1,2,5,10 \rbrace

約数の個数

約数の 個数 に注目します。一般的な特徴は以下のようになります

1の場合

1 の 1 個だけです。

素数の場合

n が素数の場合、約数は1とn自身のちょうど2個です。

合成数の場合

n が合成数の場合、約数は1とnの他にも1個以上存在します。
特に、nが平方数の場合は奇数個、そうでない場合は偶数個となります。

一般の場合

n を素因数分解した結果が p_1^{q_1} p_2^{q_2}\cdots p_k^{q_k} ( p_iは素数)として、nの約数の個数は (q_1 + 1)(q_2 + 1)\cdots(q_k + 1) となります
これを題材にした出題も、ときどき出てくるイメージなので忘れないようにしたいですね！ (今日は使いません)

(おまけ) 高度合成数

約数の個数に触れたので高度合成数というものにも軽く触れておきます。
約数の個数が多いやつは高度合成数と呼ばれて、こんな感じです
高度合成数の一覧 | アルゴ式 この辺はキラーケースになることが多いです

反比例のグラフに乗る

nの約数は、反比例のグラフy=\frac{n}{x}に乗ります。
y=\frac{n}{x} を通る格子点の x座標を列挙すると(またはy座標でも同じ)、nの約数に一致します。
下の図1では、 n=6の例で、格子点のx座標は 1,2,3,6 となり、6の約数と一致します。

図1
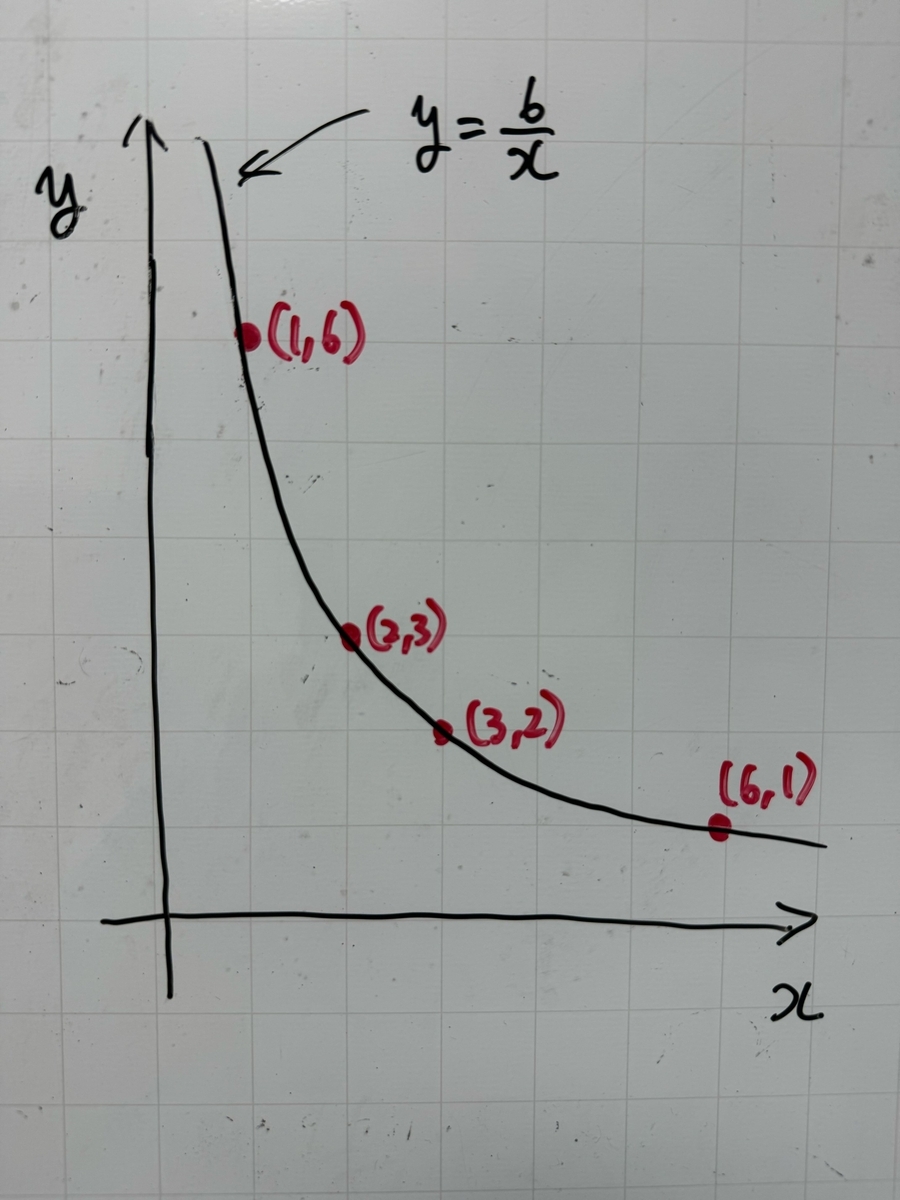
特に個数に関しても、nの約数の個数は、y=\frac{n}{x} を通る格子点の個数に一致する
というのも、個人的には忘れがち/ 見逃しがちな言い換えな気がします
例えば、6の約数は4個 ⇔ y=\frac{6}{x} を通る格子点は4個
です

本題

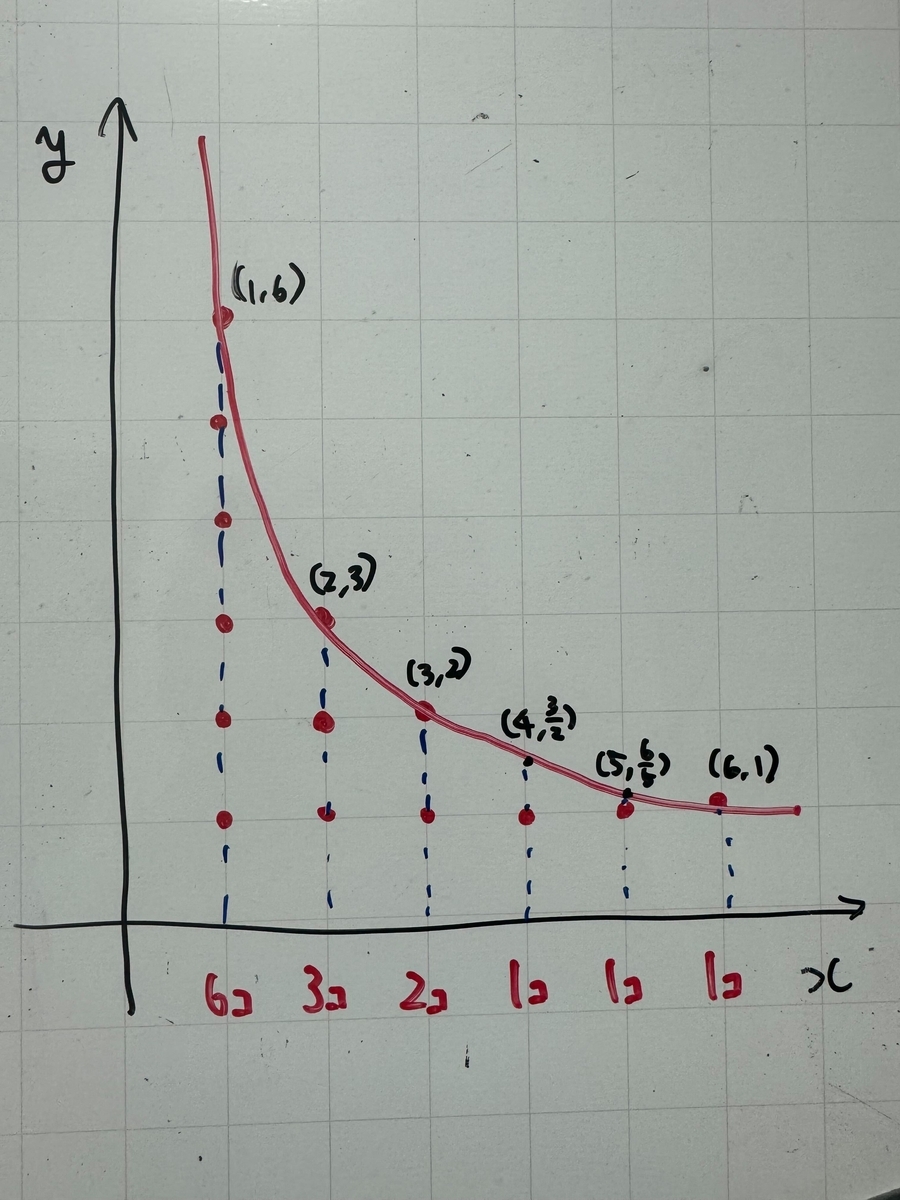
「1からNまでのnについて、nの約数の個数の総和」 を求めたいのですが、図にすると以下の図2の赤線の部分 (赤ドットの数)を数えたいです。

図2

理由としては、以下の図3を見てほしいのですが、1からNまでのnについて、先ほどの y=\frac{n}{x} のグラフを重ねていくと、Nより内側の格子点をすべてもれなくカバーしていることがわかります (図ではN=6)

図3
つまり、「1からNまでのnについて、nの約数の個数の総和」 とは、y=\frac{N}{x} のグラフの内側にある格子点の個数 と問題を言い換えることができました。

Nが小さい場合

まず N \le 10^{6} の場合を考えます。
この場合は、下の図4のように縦に数えるだけで良いです。

図4
具体的には、nが1からNにいたるまで、 \lfloor \frac{N}{n} \rfloor を足して行けば良いです　(\lfloor x \rfloor は床関数、整数切り捨て)

さて、Nが大きい場合はどうしましょう...？？？

Nが大きい場合

本題の本題です。 N \le 10^{12} の場合は、先ほどの方法では計算時間は間に合わず、大部分が計算できてないように思われます。
ところが、不思議なことにあとちょっとの工夫で求まるようになります。
キーワードは \sqrt{N} で分割する です！

個人的に一番わかりやすいアプローチはこれでした。
以下、図をABC230-E kyopro_friendsさんのユーザ解説 より引用しています

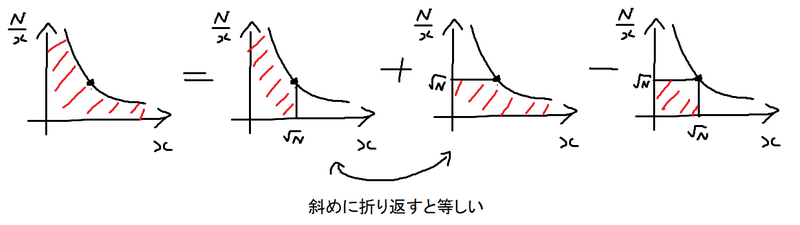
図5 Nが大きい場合 (ABC230-E kyopro_friendsさんのユーザ解説より引用)
図5を左から①②③④とします。
① = ② + ③ - ④ ということで、①が求めたいもので、②③④を求めれば良いと言っています。
そして、②と③は「斜めに折り返すと等しい」と書いてあります。
y=\frac{N}{x} はxとyが対称な形をしており、 x=y=\sqrt{N} がちょうどxとyが等しい部分になります。
そのため、②③のように\sqrt{N}で分割すると、漏れなく①の領域をカバーできます。 しかも、対称なので、②を求めて2倍するだけで③を足したことになります！
②の図はNが小さい場合のように縦に足していき、 M=\lfloor\sqrt{N}\rfloor として、1からMまでで打ち切れば良さそうですね。
最後に、ダブルカウントしている領域は④の部分だけになるので、ここは単に M^{2} を引けば良いです。
これでNが大きい場合についても、「1からNまでのnについて、nの約数の個数の総和」を求めることができました！

めでたし！

おまけ

問題リンク

  • ABC230-E

    • この記事の説明で使わせていただきました
    • 約数という言葉は出てこないですが、この記事でそのまま求めた内容です

  • ABC414-E

    • 問題を整理すると、約数の個数の総和が欲しくなります

ゆるふわオンサイト#8 Writer記

コンテスト開催記

ゴリ〜

ゆるふわオンサイト#8

先日はゆるふわオンサイト#8のご参加ありがとうございました！
コンテストサイト
解説スライド

writer記というほどwriterをしてないのですが、A,B問題を作問したので裏話などを書こうと思います
ちょうどゆるふわのゆるふわの部分ですね
第8回はC問題から牙をむいていたのでゆるふわじゃないじゃん！と思った方ごめんなさい
ちなみにゆるふわオンサイトがゆるふわではないというご指摘は方々から頂いております
ちなみにちなむとゆるふわオンサイトの「ゆるふわ」は問題が「ゆるふわ」の意味じゃないよ、というのは釈明しておきます

要は予選を突破しなくても出られるという意味で ゆるふわですよ〜ってことです
いろんな層の人に楽しんでもらえるコンテストを目指しています (本当ですよ！)
準備に割けるリソースとの兼ね合いで、問題数が多くは出せず、崖がどうしてもどこかにできてしまうのはご容赦ください🙇

以下、問題のネタバレを含みますので念のためご注意ください

A問題 Progress Report Decreasing... (200点)

問題

これがA問題で出たのはギョッとしたでしょう！(ごめんなさい)
ギョッとしていただければ幸いです^^
これより前にもう1問簡単なのが入る予定だったのですが準備の都合でカットされました
やるだけを期待していた方(?) すみません、、　

準備陣の見立てでは灰diffと茶diffの境目ぐらいを予想していました
文字列でやるのに気づかないと沼ってしまい茶diffもあり得る？とかABCではCぐらい？とか言われていました
0点で帰られる方がもしいたら申し訳ないと思い、せめてもの部分点を入れました
(結果的にBは全員に解いてくださったのでその心配はありませんでした)

作問の経緯ですが、進捗報告の%って失速するよね〜 とか 進捗報告は終盤ほど刻むよね〜 みたいな話題から生まれました
途中まで勢いよく90%までいったのに突然93%みたいに刻んでいくやつですね (社会人になってあんまりそのシチュエーションは見たことないですが、大学の研究室で見た気がします)
で、それを思い出して式をいじってたら面白い式ができたので問題にしました

それを題材にもっとひねることもできたのですが、これはこれで出力だけで問題にしました
出力だけでも地味に面倒な問題だったと思います

ちなみにどうでも良いのですが問題名の頭文字をとるとPRD...になるのお気づきでしたでしょうか
ここはPRDにしたくなってしれっと仕込んだのでした (無意味な自己顕示欲)

B問題 Edible Card Game (200点)

問題

はい、A問題より簡単だった疑惑のある、これです
ゆるふわオンサイトの本当のゆるふわの部分ですね(?)

これ、問題に対して思いつくことが値の大きい方から貪欲に取るぐらいしかなく、かつそれで正しいので、解法で迷うことはなかったんじゃないかなと予想しています
ちゃんと正当性を示すと (それはそうという結果ではあるが) 面白いと思うので、直感で貪欲した方は考えてみてください
少しでも迷ってくれたら儲けもんぐらいの理由で NやAの制約を無意味に小さくしたりして出しました

ちなみに、これの原案自体はN=2で、A問題に置かれるのを想定して作った問題でした
(A問題なのでif文だけで解けるけどやるだけは避けたい、ある程度考えさせたい、という意図がありました)
これを提案したら、一般のNでも同じ性質が成り立つから一般のNで出して、後ろに追いやった方が良いのでは？となり、PRD...より後ろに来ました

実際はN=2でもN<=1000でも難易度はほとんど変わらなかった説ありますね
問題セットが揃ったときに、Aより簡単ではないかという議論はされたのですが、誤差じゃないかということでそのままになりました
(実際どちらも同じ200点をつけています)

なお、原案はカードゲームではなくてAtCoderのレーティング (アルゴ、ヒュ) でじゃんけんをさせるものでした
ちょうど (アルゴ、ヒュ) の2次元の評価軸がある場合の序列について話題になっていたので、それにあやかって、アルゴとヒュの好きな方を先に出せるじゃんけんにしたら面白くね？という提案でした

C以降

他にいくつかABCライクな「やるだけ」問題を書いたりしていましたが今回は採用されませんでした
(自分はやるだけしか書けないので...)
解いててより楽しいのはARCライクな「考察」要素が強い問題だと思うので、そういう問題をできるだけ出そうと準備陣は頑張っていました
アンケートでは実際に好評をいただいた問題が多くて、嬉しかったです

おわり

以上です！
コンテストを楽しんでいただけたなら幸いです！
次回もきっと頑張ります！

2024年競プロオンサイト紀行

オンサイト参加記

ごり～🦍

今年は気づいたらたくさん競プロオンサイトに参加してしまいました、prd_xxx です
競プロの次の趣味を聞かれたら「競プロオンサイト巡り」と答えても過言ではないかもしれません
というわけで、今年参加したオンサイトをまとめていきます！
(食べ物メインよりの記事です)

参加したものたち

1/6,7 OUPC (大阪)

新年から2日制オンサイトで、夜行バス1泊+ホテル2泊の3日間大阪を楽しんだ！

3/9 TUPC (宮城)

1年ぶり仙台！夜行バス1泊とカプセルホテルに後泊した！

3/17 UTPC (東京)

MMさんと組んだのにノートPCを家に忘れるというオンサイトで考えうる最悪をしてしまった... (反省)

3/23,24 RUPC (滋賀)

立命館大で2Daysオンサイトが復活！コロナ明け数年ぶり！
新幹線で当日入り、ホテル2泊で3日目は観光をした！(有給休暇)

3/30 水以下コンテスト (東京)

芝浦工大で初のオンサイトに潜入！

3/31 MMA Contest (東京)

3月はオンサイト尽くしでタフな毎日だった！充実しまくり

8/25 MMA Contest (東京)

しばらくオンサイトが開いたと思ったらまた調布の電通大！
nafmoさん皆さんいつもありがとうございます

8/31 Maximum-Cup (埼玉)

9/15 KUDUPC (京都)

京都産業大学で初のコンテスト！ コンテスト自体は1日ですが前日のABC、当日の短期AHCに出るためちゃんと前泊と後泊しました

10/12 緑以下コンテスト (東京)

青山学院大学での開催は2回目かな？渋谷でぶやぶや！

11/17 ITF.PC (茨城)

つくば！TXで日帰りで行ける距離なんだけど、去年前泊したら楽しかったので、無駄に前泊と後泊をした！(月曜は有給休暇)

12/15 TTPC (東京)

TTPCとしてはこれまでは開催されてたけど、東工(科)大の敷地に入ったのは初めて！
大岡山でおおおおお

開催したものたち

ゆるふわオンサイト、を会社の競プロ部でやってます
お越しくださりありがとうございました！！

2/10 ゆるふわオンサイト (東京)

9/28 ゆるふわオンサイト (東京)

お寿司とピザをとったんですが、画像がありませんでした :pien:
みんな写真撮ってXに投稿して！(お願いします)

最後に

ゆるゆるっとした飯テロ記事になってしまったかもしれません
競プロオンサイト情報というXアカウントをやっていますのでぜひフォローを！
そしてオンサイトの情報募集しています！
オンサイトは良いぞ！

円環ライブラリ？？を書いてみました

Python スニペット ABC

ごり〜

こんばんは
前回のABC-376 のBやFで、円環を扱う問題が出ましたね
ゴリはB問題の段階で頭を使いたくないな〜と思った挙句に実際に時計回り/反時計回りにwhileで回す というパワープレイでどうにかACを取りました
が、それでも11分ぐらいかかっちゃったので、あんまり頭を使わない方法を考えていました
TLで 円環ライブラリ を作った、とかの声をちらほら見た気がして、どういうのがあれば楽だったんだろうと自分なりにも考えてみました
それを残します

RingCalculator

というのを作りました。
ごりちゃんライブラリにあげてあります →こちら
使い方なども↑を参照して欲しいのですが、
dist_clockwise(x,y) で、xからyまで時計回りで回ったときの距離、
dist_anticlockwise(x,y) で、xからyまで反時計回りで回ったときの距離
がそれぞれ求まるようにしています。　

これがあると例えば、xからみて時計回りでyの方がzよりも近いか？(xからyまでの時計回りの中にzが含まれていないか？) を以下のように判定することができます

rc.dist_clockwise(x,y) < rc.dist_clockwise(x,z)

そして、ABC376-B は以下のコードでACできます。提出
何気に1-indexed にも対応してます (デフォルトは0-indexed)

# https://github.com/prd-xxx/gorichan_kyopro_library/blob/main/ring_calculator/ring_calculator.py
class RingCalculator:
    def __init__(self, size, base_index=0):
        self.size = size
        self.base_index = base_index
    def _normalize(self, index):
        return (index - self.base_index) % self.size
    def dist_clockwise(self, from_index, to_index):
        fr = self._normalize(from_index)
        to = self._normalize(to_index)
        return (to - fr) % self.size
    def dist_anticlockwise(self, from_index, to_index):
        return (self.size - self.dist_clockwise(from_index, to_index)) % self.size

N,Q = map(int,input().split())
HT = [input().split() for i in range(Q)]

rc = RingCalculator(N,base_index=1)
ans = 0
l,r = 1,2
for h,t in HT:
    t = int(t)
    if h=='L':
        if rc.dist_clockwise(l,t) < rc.dist_clockwise(l,r):
            ans += rc.dist_clockwise(l,t)
        else:
            ans += rc.dist_anticlockwise(l,t)
        l = t
    else:
        if rc.dist_clockwise(r,t) < rc.dist_clockwise(r,l):
            ans += rc.dist_clockwise(r,t)
        else:
            ans += rc.dist_anticlockwise(r,t)
        r = t
print(ans)

おわり

これだけでした
ちょっとしたコードだけど多分次使うときにはありがたみを感じてると信じたい！

ゆるふわオンサイト#7 Writer記

概要

ゆるふわオンサイト#7 の、BCDI の Writerをしました
作問の経緯や裏話を書いていきます (ネタバレ注意！)

コンテストページは以下です
ゆるふわ競技プログラミングオンサイト at FORCIA #7 | MOFE

解説スライドはこちらです

B - Group Moving

B - Group Moving

Writerの想定は灰〜ギリ茶色diffぐらい、ABCならC問題で300点ぐらいの想定でした
(200点ってつけてたのでびっくりした人はごめんなさい)
「全部言われた通りに愚直にやるとTLEするけど、ちょっと工夫すると解ける」って難易度帯を作りたくて作りました
クエリを色ごとに集計しておけば、あとは順に適用していけば間に合う、ってネタでしたがいかがでしたでしょうか？
C++ だと負のmod演算やオーバーフローなど、罠がたくさんあったようで苦戦した人すみません。
あとはネクタイをつけたゴリラというのはもちろんドンキーコングさんリスペクトです

C - Proper Fraction Operation

C - Proper Fraction Operation

Writerの想定は茶色diff、ABCというよりはARC-A とかにあるかも？という感じを想定していました
ちょっと紙に書いたり実験をするとわかる系で入門的なものを作ってみたつもりでした
K = 1のケースを入れていたり、K = 1 でA/B が既約でないケースを入れてたのは引っかかる人いるよな〜とは思いつつわざと入れていましたが思った以上にペナってる方がいてすみませんという気持ちになりました
あとはなんか意外と難しかったみたいで実装方針によっては通すのが大変そうでした
コンテスト中、控え室でもスタッフが裏で解いていたのですが、A〜Eまで通した中で一番Cに苦戦してそうでした
思ってた以上に大変そうですみません　ペナらずに解けた人はえらいです！

D - Taking Sandwitches

D - Taking Sandwitches

これどうやって問題を生やしたのか覚えてないんですが、最初は数列Aは長さが2Nで、1〜Nの値が2回ずつ登場する、という設定でした
想定解は同じで、左からdpだったのですが、「2回ずつしか登場しないって制約は無くせる」とある暖色コーダーから指摘があり、Aの入力にバリエーションがある(その分工夫もいる) 面白い問題になったと思っています
あと、「最短路問題としても解ける」と別の暖色コーダーから教えてもらったときは面白い問題だな〜って我ながら思いました
A \le 2 の部分点は思いつきで後から提案したのですが、「意外とパズルっぽくて面白い」という評価があり、採用されることになりました
アンケートで好きな問題としても票を集めていて、嬉しかったです 　

I - FORCIAN WAY

I - FORCIAN WAY

これのWriterなのびっくりですよね...
作問チームの想定では橙diffはあるだろうという意見が多く、ボス枠GHIの中で一番難しいということでラストにおかれました
(H問題のほうがTesterが苦戦されていたのですが、H問題のWriterが絶対にIの方が難しいと主張されていたので、こうなりました)
この問題が生まれた経緯ですが、最初は嘘解法の原案でした
2000\times2000 のグリッドで同じ問題だったのですが、「 2000\times2000\times6のメモリを持ってBFSさせれば解ける」という想定が、ある暖色コーダーの指摘で「単純なBFSだと解けない、例えば空白マスをFとして通ったことを保持しないとその後にRとして通ってしまうかもしれない」と指摘されて爆破されました。　 (実際にBFSで解こうとするとサンプル3でYesになると思います)
で、爆破された後しばらく解法が存在しないまま原案置き場に置かれていたのですが、別の暖色コーダー2が「縦を3行にすると面白くなるかもしれない」と提案し、別の暖色コーダー3が華麗な解法 を示してくれました。　
ゴリはもちろん自力で解けなかったので、Writer解()は暖色コーダー3さんに手取り足取り教えてもらってやっと書けました
コンテストまでに複数人に解いてもらえて、テストケースも頑張って強化できたので、自信を持って出すことができました。
この問題の面白いところは、難易度の割にかなり「とっつきやすい」見た目をしていて、難しい知識もいらなく、考察の積み重ねで解法に至れる可能性があるところだと思っています。なので、(自分は解けなかったが) 水色コーダーでもたくさん時間を掛ければできるやつだと思っています
こういう面白い問題を出せたのは、自分だけの力では無理で、作問チームの皆さんのおかげだと思っています
以前のブログ でも述べたのですが、チームで作問をするとこういった「自分の原案が強化されてより完成度の高い問題ができる」という経験ができるので、大変楽しいです。
FO社でゆるふわの作問に参加してくださるメンバーを引き続き募集しています。　

まとめ

前回ゆるふわ#6では自分の原案が採用されなかったのでTester寄りの役目をしていましたが、今回は4つ採用されたので4問のWriterになりました。
作問チームで多種多様な議論や指摘をしてもらえるので、最初の原案より完成度が上がり、作問経験として満足度が高いです。　
(ペナを出させちゃって苦しめた問題もあったかもですが) 概ね参加者からのコンテストの評価も高く、作問に関われて良かったなあという気持ちです。　
今後も開催していく予定ですので何卒よろしくお願いします。　

「K番目に⚪︎⚪︎」のにぶたん(二分探索)への直し方

アルゴリズム Python

先日こんな問題が出ました ABC364-D K-th Nearest

(概要)

数直線上にN個の点があるので、以下のクエリにQ個答えてください。

  • N個の点のうち座標xからK番目に近い点との距離を求めよ

NもQも{10}^5ありうるので、愚直に調べるのはTLEします。

じつは

  • K番目に近い点の距離を求めよ

という問題はにぶたん (二分探索) が相性が良いです。

にぶたんで解ける問題にするために、問題の言い換えが必要なのですが、
これは筆者がとても苦手としていて毎回10分ぐらい悩むので、次に出てきたら使えるようにメモしておきます。
以下が結論です。　

  • xからK番目に近い点の距離を求めよ

↓(言い換え)

  • 「xから距離d以下の点が何個ある？」の答えがK個以上になる最小のdはいくつ？

です。
どういうこと？ほんとにそうなの？は後述するとして、この言い換えができれば
「距離d以下の点が何個ある？」の問いに高速に答えられれば、にぶたんが使える！となります。

実際、この問題ではxの左右両側を調べる必要がある点に注意ですが、
xとdが決まっていれば
bisect_right(A, x+d) - bisect_left(A, x-d) 等のようにすれば「xから距離d以下の点の個数」が求まります
これを使ってにぶたんをすると問題をACできます (にぶたん in にぶたん 1)

どういうこと？ほんとにそうなの？

左右を見る問題はちょっと複雑なので単純にします。

距離に限らず、比較可能な数値であれば適用できます。
ソートされた数列があり、これの「小さい方からK番目」を求めることにします。2

A = [1,2,2,3,4,4,5,6 ]

これの、
「小さい方からK番目」の値
と、
「a以下の値は何個？」の答えがK個以上になる最小のaはいくつ？
の答えが一致することを確認します。

まず、a以下の値は何個？を小さい方から調べてしまいます。　

  • 0以下の値は？: 0個
  • 1以下の値は？: 1個
  • 2以下の値は？: 3個
  • 3以下の値は？: 4個
  • 4以下の値は？: 6個
  • 5以下の値は？: 7個
  • 6以下の値は？: 8個

のようになっています。　
例えば K=4のときを見ていきます。　
aが小さい方から見ていって、a以下の値は？が初めて4個以上になるのは、確かにa=3の時で、Aの4番目の値は3です。　
また、K=5のとき、　
a以下の値は？が初めて5個以上になるのは、a=4の時で、Aの5番目の値は4です。　
同様に、K=6のとき、
a以下の値は？が初めて6個以上になるのは、a=4の時で、Aの6番目の値は4です。　

他の場合を試しても、確かに言い換えが正しいことがわかります。3　

(おまけ) 言い換えのバリエーション

  • 「スコアが小さい方からK番目の人」を求めよ

↓ (言い換え)

①「スコアa以下の人は何人？」の答えがK人以上になる最小のaはいくつ？
②「スコアaより大の人は何人？」の答えが(N-K)人を超えない最大のaはいくつ？
③「スコアa以上の人は何人？」の答えが(N-K+1)人以上になる最大のaはいくつ？
④「スコアa未満の人は何人？」の答えが(K-1)人を超えない最小のaはいくつ？

  • 「スコアが大きい方からK番目」「大きい方からK位」の場合は以下の通りです。

↓ (言い換え)

⑤「スコアa以上の人は何人？」の答えがK人以上になる最大のaはいくつ？
⑥「スコアa未満の人は何人？」の答えが(N-K)人を超えない最小のaはいくつ？
⑦「スコアa以下の人は何人？」の答えが(N-K+1)人以上になる最小のaはいくつ？
⑧「スコアaより大の人は何人？」の答えが(K-1)人を超えない最大のaはいくつ？

頑張ってバリエーションを考えてみたものの、とりあえず①と⑤があれば良さそうですかね。^^

おわり

にぶたんマスターになろう！

  1. 界隈では「log2つ」とかよく言われますね　NやlogNの大きさなどにもかなりよりますが、2つまでならPyPyでギリギリ通るようになってることが多いです↩
  2. 「小さい方からK番目」「小さい方からK位」ときたらこのパターンを引き出せるようにしたいですね↩
  3. もっと論理的な説明ができればかっこよかったんですが「実例を確認する」にしてお茶を濁したゴリラです...↩

大きい方/小さい方からtopKを管理しながらなんかやるモジュールを書いた

Python スニペット

ごり〜　（こんばんは)

なんか書きました
大したものじゃないんですけどたまによくデータ構造系のやつで「heapq2本持ちながらやる」みたいによく言われるやつです
実装の都合でheapq2本ではなくtatyamさんの「SortedMultiset」を2本持つ形で実装しています
heapqじゃないので速度は期待しないでください (代わりにSortedMultisetの部分は高機能です)
コンテスト中に書いてもいいぐらいのコードだけど、たまに出てくる気がするのでペタりできたほうが嬉しいよね

今回ご紹介するのは

こちらです、 TopKSortedMultiset
詳しくは上記リンク先に書きましたが、自由に追加/削除が O(√N) ででき、任意の時点でtopK個の和などが取れます
和じゃないものが必要になったら適宜改造して使ってください☆★☆★(なぞの星)

使い方実例、verify

ABC281 E - Least Elements

各A_i から A_{i+M-1} までのうち小さい方からK個の和を高速に求める問題。
切れ味抜群です。

Submission #53027580 - AtCoder Beginner Contest 281

N,M,K = map(int,input().split())
A = list(map(int,input().split()))
ts = TopKSortedMultiset(K, A[:M], mode_max=False)
ans = [ts.sum_topk]
for i in range(M,N):
    ts.add(A[i])
    ts.discard(A[i-M])
    ans.append(ts.sum_topk)
print(*ans)

ABC306 E - Best Performances

クエリごとにA_{x_i} を y_iに書き換えていき、大きい方からK個の和を求める問題。
これも切れ味抜群。

Submission #53027660 - Toyota Programming Contest 2023#3（AtCoder Beginner Contest 306）

N,K,Q = map(int,input().split())
XY = [tuple(map(int,input().split())) for _ in range(Q)]
A = [0] * N
ts = TopKSortedMultiset(K, [0]*N)
for x,y in XY:
    x -= 1
    ts.discard(A[x])
    ts.add(y)
    A[x] = y
    print(ts.sum_topk)

Donutsプロコンチャレンジ2015 - ドーナツの箱詰め

このモジュールを作ろうと思ったきっかけになった問題。
やることが整理できていれば実装は楽になるはず

Submission #53003393 - Donutsプロコンチャレンジ2015

N,K = map(int,input().split())
C = list(map(int,input().split()))
Q = int(input())
qs = [C[int(input())-1] for i in range(Q)]

ss = SortedSet(C)
ini_arr = []
p = None
for c in ss:
    if p is not None:
        ini_arr.append(c-p)
    p = c
ts = TopKSortedMultiset(K-1, ini_arr)
print(ts.sum_other)

for q in qs:
    ss.discard(q)
    l = ss.lt(q)
    r = ss.gt(q)
    if l is None:
        ts.discard(r-q)
    elif r is None:
        ts.discard(q-l)
    else:
        ts.discard(r-q)
        ts.discard(q-l)
        ts.add(r-l)
    print(ts.sum_other)

できそうでTLEしたやつ (ざんねん)

今後の課題

ABC234 D - Prefix K-th Max

ふつうにheapqでやりましょう...

Submission #53027482 - AtCoder Beginner Contest 234